

301 Moved Permanently
System monitoring companies typically have very large portfolios of performance data and are in particular need of effective methodologies for identifying underperforming systems.
The most common approach to determine potential underperformance is to calculate a performance metric for each system by dividing the measured actual energy production by what the energy production should have been. The vagueness about “should” is intentional here because different answers give different performance metrics, all of which have their own trade-offs.
Let’s take a deep dive into three possible values of the energy that should have been produced for a site:
i. Expected energy: This is the upfront design’s estimated energy calculated from the system’s design, expected insolation from a design weather file (e.g., from TMY3) and a PV model (e.g., PVWatts, PVsyst, SAM).
ii. Weather-adjusted expected energy: This is the expected energy adjusted by the ratio of the actual irradiance to the expected irradiance.
iii. Modeled energy: This is calculated with a PV model using the actual weather conditions as inputs.
Our analysis confirms the intuitive suspicion that these methods are increasingly accurate as you go from i to iii. Attempts to characterize how accurate these metrics are and what drives the errors in each of them found the following broad conclusions:
1. Accurately modeling energy production with a PV model is very difficult and is typically the largest source of error if default derates are used;
2. If design expected energy is used without weather adjustment based on actual weather, typical weather variations will be a comparably large source of error to #1;
3. Acquiring accurate insolation data is difficult, and even with state-of-the-art techniques, it is the second-largest source of error after #1 (this error is incurred instead of the larger error in #2);
4. Using global horizontal irradiance (GHI) instead of plane of array irradiance (POAI) to ratio adjust is a relatively small source of error; and
5. Using a POAI ratio instead of running a PV model on the full weather data time series (i.e., linearizing the PV model) is a relatively tiny source of error.
As a result of this, for Locus Energy’s own projects to identify underperforming residential and commercial systems, we use a weather-adjusted energy expectation ratio as our key performance metric and have focused our efforts on minimizing the PV modeling and irradiance errors.
Without any further ado, let’s get into the details. I hope you like math!
What’s a GEER?
To make a weather-adjusted performance ratio precise, define the GEER (GHI-adjusted Energy Expectation Ratio) as follows:
GEER = Energyactual / Energyexpected / ( GHIactual /
GHIexpected )
where GHI is the global horizontal insolation.
As an aside, you can use a satellite-derived virtual irradiance number in lieu of an on-site irradiance sensor for GHIactual. This is a critical point considering that the motivation for this analysis is to identify underperforming systems, many of which will not have physical irradiance sensors.
The first big question to address is how good of a proxy the GEER is for a performance index (PI) based on running an industry-standard PV model like PVWatts or the five-parameter model (for simplicity, assume these are all equivalent).
Specifically, if it’s said that PI = Energyactual / Energymodeled,
then if you divide and cancel the measured energy terms, you see that
GEER / PI = Energymodeled / Energyexpected / ( GHIactual / GHIexpected ).
The methodology we used to investigate this quantity considered the historical hourly meteorological data from the National Solar Radiation Data Base (NSRDB) for all 242 Class I sites for the period of 1995-2010 and the TMY3 data for these locations.
First, use the Erbs coefficients and the Hay-Davies transformation to calculate POAIs for 50 tilt and azimuth configurations that regularly sample those seen in our North American fleet (i.e., azimuths between SE and W every 15 degrees and tilts between 0-40 every 10 degrees).
Next, use the PVWatts model to generate hourly modeled energy for all of the sites and configurations and aggregated to the monthly level. Finally, do the same thing for the expected energy.
At this point, you know what the modeled and expected energy and GHI would have been for a broad sampling of panel orientations over a 15-year historical period. This allows you to calculate the monthly GEER / PI historically to get a grasp on how different these metrics are.
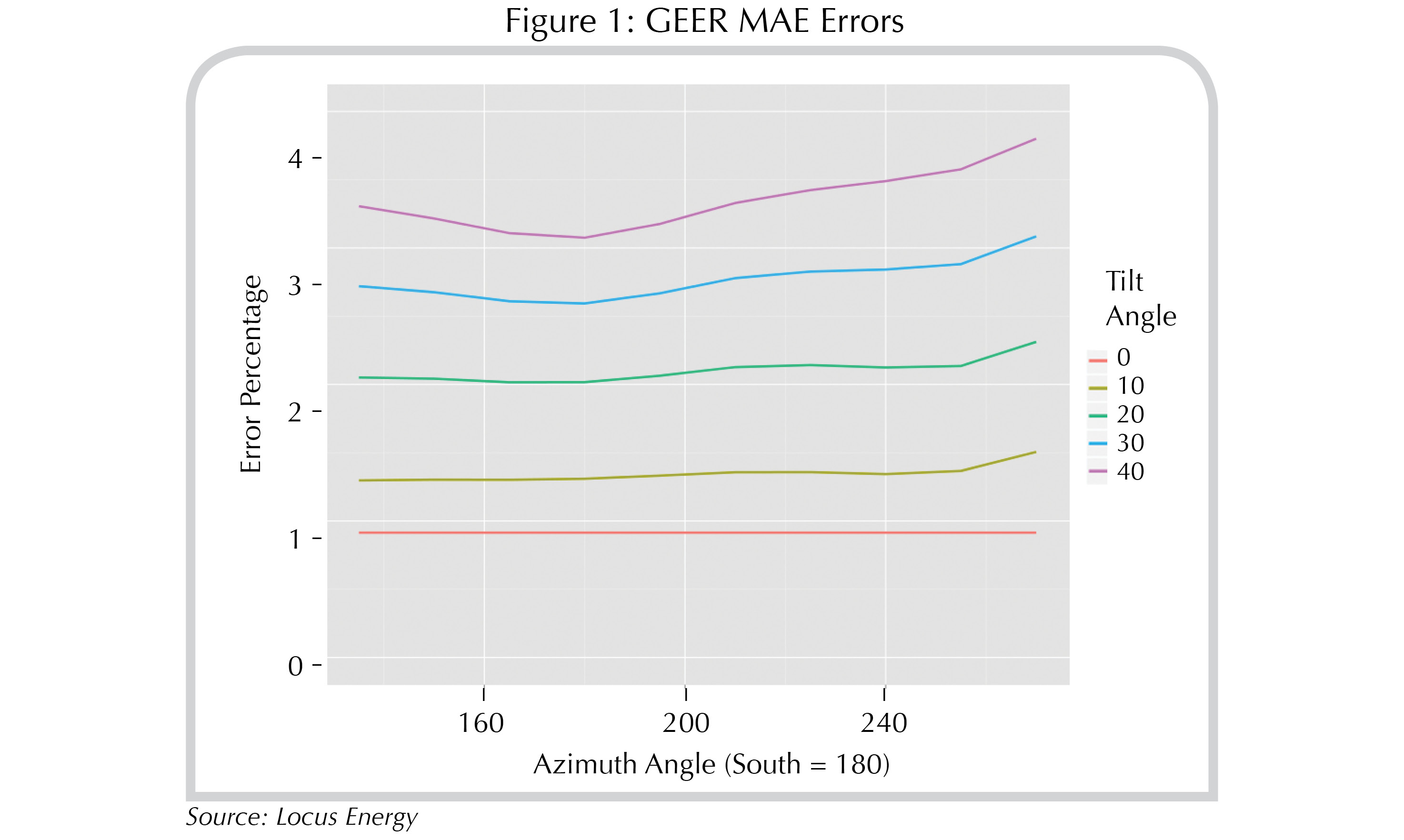
Defining the error as 1 - GEER / PI, aggregating by tilt and azimuth, and calculating mean absolute error (MAE) percentages, you get the plot as shown in Figure 1.
The first big takeaway from the plot is that the errors increase primarily with tilt and secondarily with azimuths that differ from directly south facing. This squares nicely with the intuitive expectation that this error should be driven primarily by the difference between monthly POAI and GHI.
The second big takeaway is that if you were curious about the error that should be expected if one used a POAI instead of GHI for the irradiance adjustment, this is an identical calculation to the tilt 0 case. Therefore, an MAE of around 1% should be expected as the difference between ratio adjusting with POAI data instead of re-running the full PV model (i.e., linearization).
The final takeaway from the plot is that the errors don’t seem particularly large. Empirically, the most common tilt and azimuth configurations that you see correspond to MAEs in the 2%-3% range.
This leads to another question: How important is that 2%-3% in the context of identifying underperforming systems?
The error in GEER
Now let’s consider the question of what the distribution of GEERs is for a fleet of systems that are functioning correctly. To get a handle on this, you need to consider the other two sources of error that are going to affect the GEER in a real-world scenario:
1. The error in the satellite-derived GHI estimates that you are using in lieu of irradiance sensors (irradiance sensors are not economical for residential sites and are often unreliable otherwise); and
2. The error between the modeled energy and the measured energy that you would expect to see even if you had perfect meteorological data.
If you are willing to do a little bit of algebra, throw out some higher order terms in Taylor series expansion, and make some calculated assumptions about the statistical independence and normality of some errors, you can get to the following equation for the expected distribution of the GEER for systems that are performing as expected (e.g., no broken inverters, system degradation):
GEER ~ 1 + EVI + Econv + Emodel
where EVI is the % error that is seen for monthly virtual irradiance estimates; Econv is the % error from the previous section due to converting from GHI to POAI and linearizing; and Emodel is the % error between a PV-modeled energy and measured excluding irradiance error.
Further, all of the E terms are gaussian noise under these assumptions. The upside of breaking down the errors this way (and making all of those assumptions) is that you then get the following relationship between the statistical variances:
VarGEER = VarVI + Varconv + Varmodel
The variance of the GEER is just the square of its standard deviation.
Conveniently, you already have error metrics on virtual irradiance from our prior work (~4.5% standard deviation at the monthly level). Note that the standard deviation of the error is not the most common measure for describing GHI errors, and it is being used here because of the additivity of variance relationship being utilized. This error percentage would be closer to 2.5% if stated as an MAE percentage. You can estimate Varconv as roughly 2.5% utilizing the calculations in the previous section.
Varmodel has thankfully already been addressed by a number of authors, including the National Renewable Energy Laboratory, Sandia National Laboratories and Locus Energy.
The results differ from author to author according to the exact methodology used, for example:
1. For well-maintained systems free of soiling and shading with carefully chosen derates, the standard deviation of the monthly energy error can be as low as 5%; and
2. For a broad sample of real-world systems that experience soiling, shading and snow cover using the default derates for all systems, the standard deviation of the monthly energy error inclusive of irradiance error was estimated at 16%.
This divergence in results matches the observation that the accuracy of PV models is highly dependent on using rigorously determined system-specific derates instead of simply using the defaults. This has been observed both in the literature and empirically by fleet operators.
Consider the two following cases:
In the first case, where you have carefully chosen derates, combining the 4.5% standard deviation of the irradiance error with 5% from the PV modeling implies an estimated standard deviation of 6.7% total modeling error. If you further combine the 2.5% standard deviation from the conversion error, you get 7.2% as expected GEER standard deviation. Thus, there should be ~7% more noise in the GEER estimated compared with a well-calibrated PV model (7.2% vs. 6.7%).
In the second case, where default derates are used, combining the 2.5% standard deviation due to the conversion error with the 16% standard deviation combined error from the PV modeling and irradiance error implies a GEER error with a 16.2% standard deviation, or a ~1% increase.
In either case, however, the relative increase in error that you get from using a GEER in place of a PV model is less than 10%. This increase in error seems manageable, given the benefits of using a GEER instead of running a PV model. Note that the increased error from using default derates (i.e., 16% vs. 7%) is roughly an order of magnitude greater than the error increase due to using GEER instead of a PV model.
It might seem like we are largely re-stating the results of the previous section of this article at this point, but all of these assumptions and calculations allow us to make reasonable estimates of how accurate these metrics are on an absolute basis instead of merely on a relative basis. This allows you to tie in the analysis of GEER and PI to an analysis of how a non-weather-adjusted energy expectation ratio should perform.
Why even weather adjust?
Let’s start by defining the energy expectation ratio as the following:
EER = Energyactual / Energyexpected
This metric is even easier to calculate than GEER (you don’t need virtual irradiance) and is a contractually important metric for many systems. If you subject this metric to our previous analysis, we would expect the error of this metric to be a combination of the error that you get based on the weather in a specific month differing from the long-term average (i.e., how different will December 2015 be from a typical December?) and the error due to PV modeling, which we considered earlier. Specifically,
EER ~ 1 + Eweather + Emodel
where Eweather is the % error that we see between actual insolation and the long-term average and Emodel is the % error between a PV-modeled energy and measured excluding irradiance error.
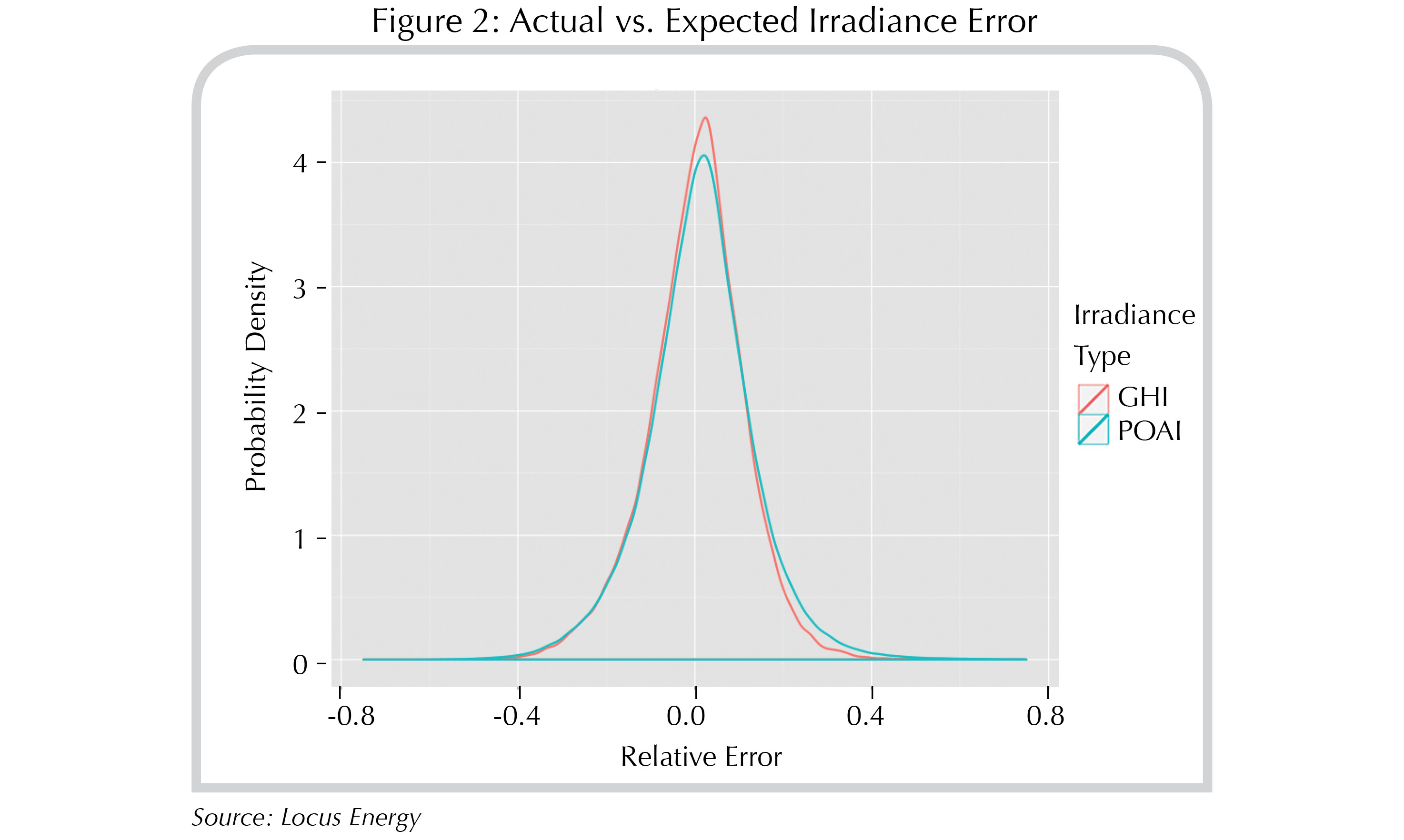
The calculations on the NSRDB data in the previous section make estimating this monthly weather variation extremely easy. In fact, the distribution looks like Figure 2.
The standard deviation of this distribution (GHI) is roughly 11%. For context, the standard deviation of the monthly virtual irradiance error distribution is estimated at 4.5%. Tying this back to the cases in the previous section, in the case where we use carefully chosen derates to get our expected monthly energy, you should expect the standard deviation of error for an EER near 12% compared with 7.2% for GEER (-40%), and for default derates, you get 18% instead of 16% (-11%).
Thus, if the PV modeling errors in your expectation generation calculation are typical for default derates, the improvement in accuracy that you get from using a GEER instead of EER is noticeable but not huge. However, if you are modeling sites with carefully chosen derates when the expectations are generated, then GHI adjusting your energy expectation ratio should provide a massive 40% reduction in error.
To sum everything up, the biggest takeaway from this article is that the largest drivers of error in performance metrics for PV systems are the modeling error due to the difficulty of accurately estimating derates and irradiance errors. Ratio adjusting with insolation instead of running a full PV model adds only a very small amount of error. Using GHI instead of POAI also adds only a relatively small amount of error.
The upshot of all of this is that with access to both high-quality irradiance data (e.g., virtual irradiance) and accurately estimated derates, it is possible to calculate performance metrics for a very large number of sites with high accuracy.
System Monitoring
Understanding Errors In PV Performance Metrics
By Charles McBrearty
Accurately and efficiently modeling as-built PV system performance is difficult on many levels.
si body si body i si body bi si body b
si depbio
- si bullets
si sh
si subhead
pullquote
si first graph
si sh no rule
si last graph